Fókuszban a térsarok. Tér-szerkesztés szabadkézzel

Hogyan alakítható tér-szerkesztés tárgy-rajzolássá? 

(Y-csomópont helyreállítása vetületekből)

Kulcs-szavak: átlós módszer, felezősík, köztes ferde, látókúp, mag-kocka, négyzethálós nagykocka-belső, nézőpont, oldalmetszék-arány, papírcsík-módszer, segédvetület, szélső ferde, szerkezeti alapvonal-háló, tárgy-képsík, térsarok, térsarok-mérce, vezérsugár, Y-csomópont.

A Budapesti Műszaki és Gazdaságtudományi Egyetem építészkarán, 2005 tavaszán, a harmadévesek számára kiadott szerkesztési feladat az "új" Műegyetem hosszanti aulájának látványterve volt (Tervezők: Varga Levente - Molnár Csaba - Peithy Attila - Répás Ferenc).

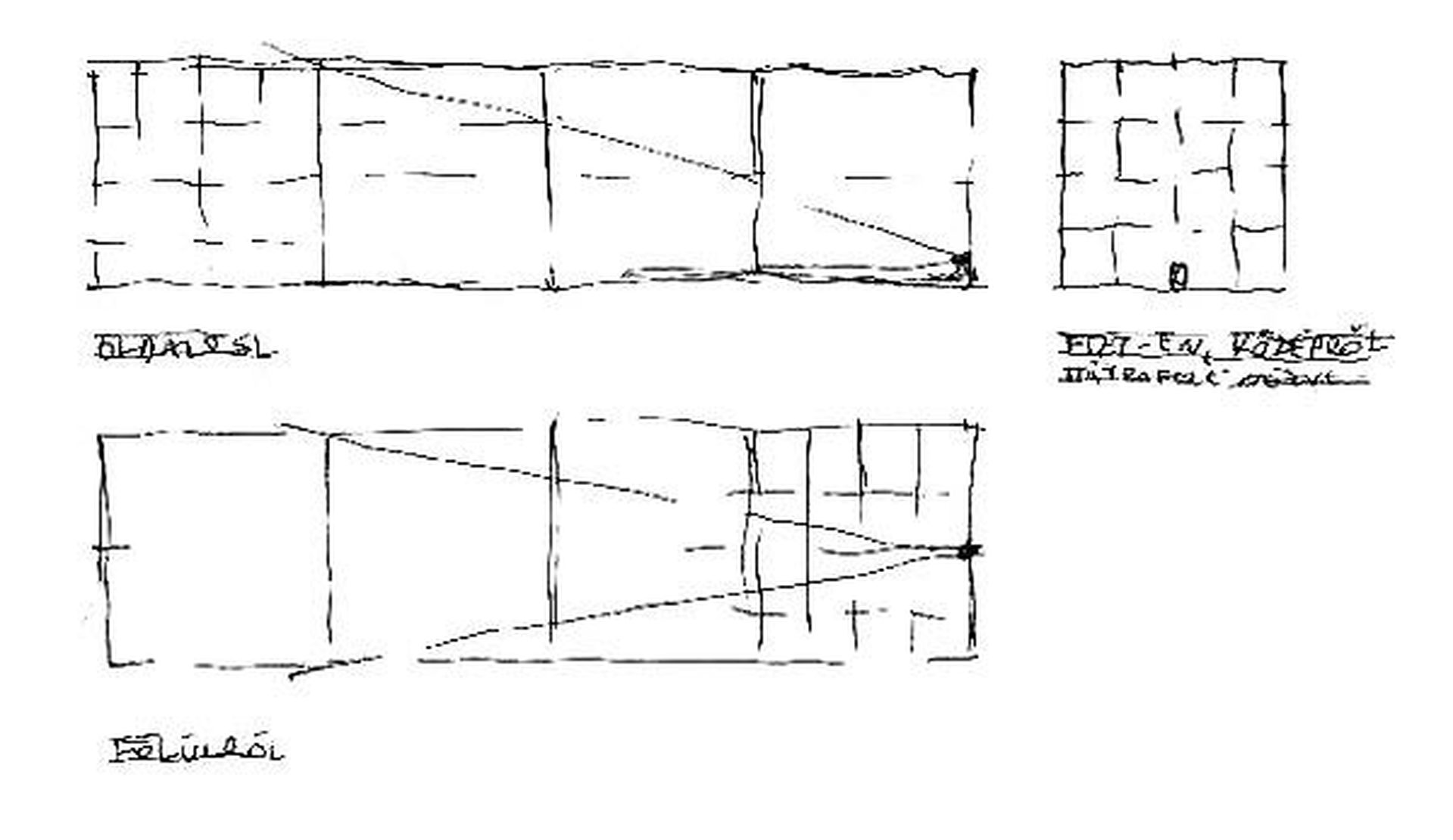
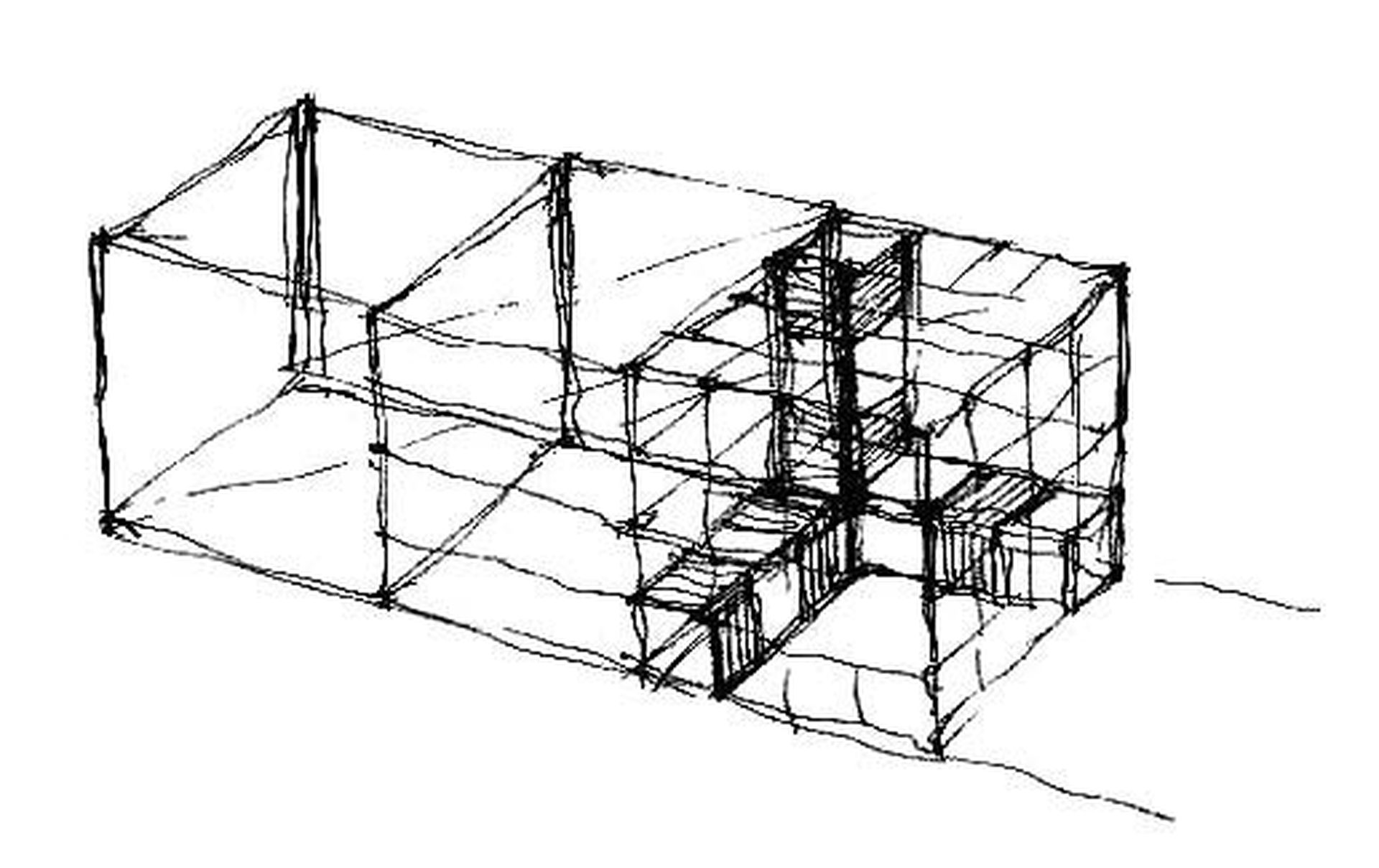
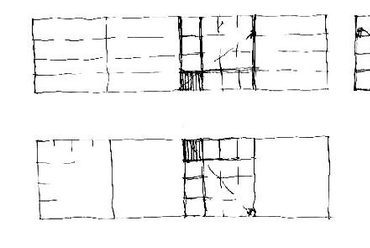
A távlati kép szerkezeti alapvonal-hálójának létrehozása kedvéértmindenek előttegyszerűsítenünk kell. A vetületekre négyzethálót terítve, kirajzolódik a térbe írható nagykocka-sor. A következőkben "egy négy-kockányi térnek" különböző látószögekből elképzelt perspektíváját mutatjuk be. Választott nézőpontjaink:

1. Alsó szint közepén állva, messze előre tekintve;
2. középmagasan, oldalfal mellől, egy távoli sarok felé fordulva;
3. középmagasan, oldalról, egy azonos szinten lévő, közeli sarok felé;
4. felső szint sarkából, közeli sarok felé lenézve.

Építészeti szabadkézi rajzban legyen számunkra a TÉR: "négyzethálós nagykocka-belső".

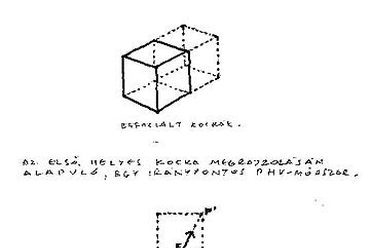
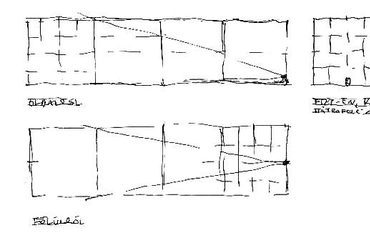
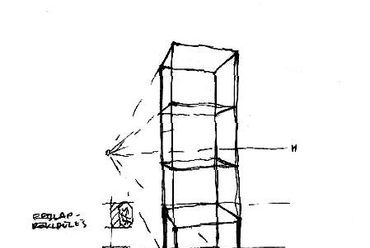
1. ábra: Az "átlós módszer" illusztrációja. "Az ábrázolandó teret kockahálóba foglaljuk. Az első kockát szabadkézzel vázoljuk fel oly módon, hogy perspektívája megfeleljen választott nézőpontunknak. A kívánt végeredményt szem előtt tartva, előzetes tömegvázlatok révén juthatunk el látószögünk kiválasztásához. Talán nem túl nehéz feladat fejből kockát rajzolni azoknak, akik természet után elegendő hasonló beállítást rajzoltak végig! Az átlós módszer segítségével a további részletek innen kezdve szabályosan szerkeszthetők."*

* Dr. Méhes B.: "Egy iránypontos perspektíva helyreállítása vetületekből, az első, szabadkezes kocka révén", 2003 [1]

Ha fentieket a "perspektíva helyreállítása vetületekből" (PHV) típusú, építészeti szabadkézi rajzfeladatok megoldására elfogadjuk, akkor bármilyen bonyolult tér-szerkesztést egyszerűbben kezelhető tárgy-rajzolási teendővé alakíthatunk vissza.

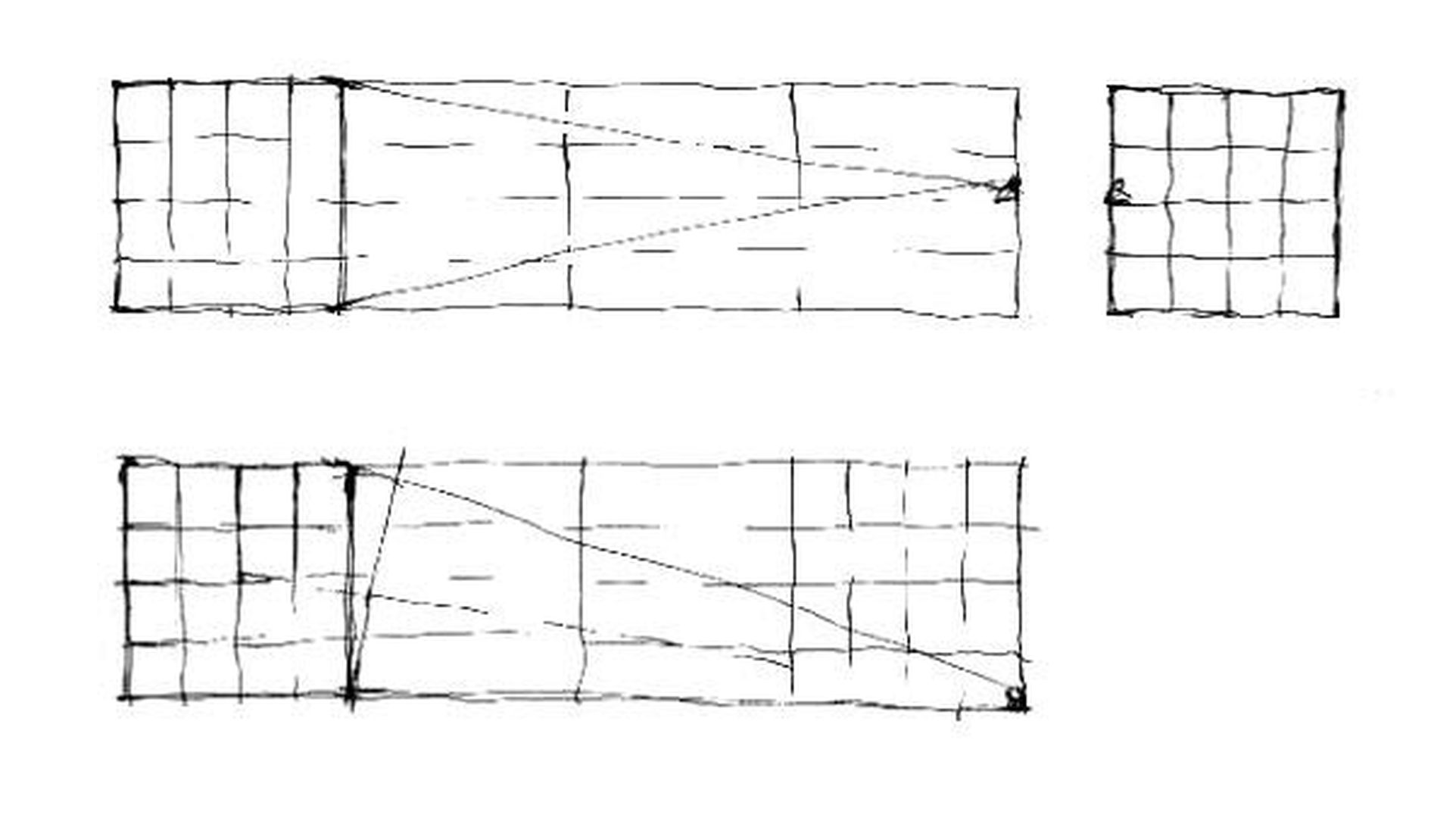
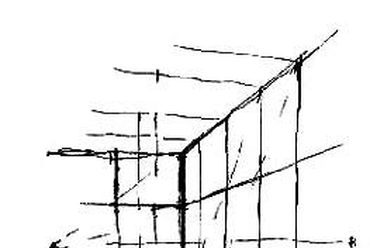
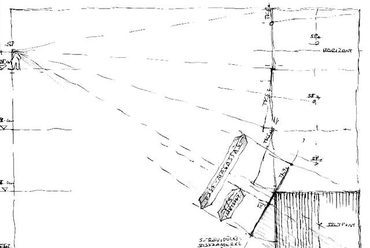
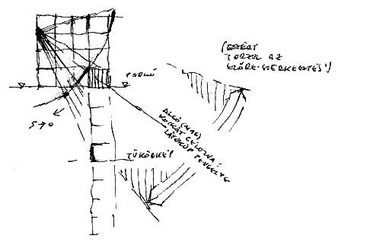
5. ábra: A (B) helyzethez tartozó látvány képe. Amint a központi iránypont kicsúszik a szemközti falról (l. az előlap és a képsík viszonya**), a szerkezeti rács szélső vízszintesei megbillennek.

**Dr. Méhes B: "Tükröződő torony trió - a szerkezeti rács szélső lapjai", 2004. [2]

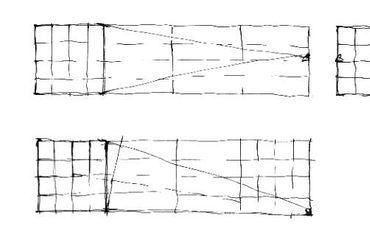
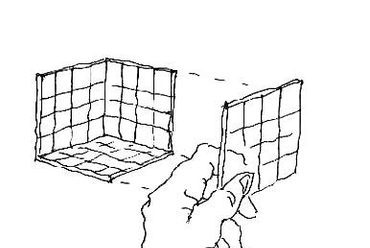
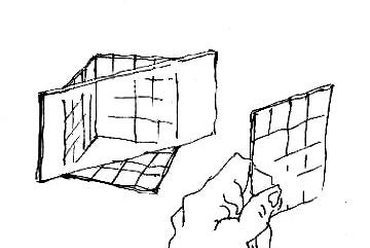
6. ábra: (C) eset, két iránypont - félmagasságból, oldalt a fal mellett állva, közelebbre tekintve.

7. ábra: A (C) helyzethez tartozó látvány. Amint a központi iránypont szemből elmozdul, a szerkezeti rács eredeti vízszintesei megbillennek - a második iránypont oldalról lassan bekúszik.

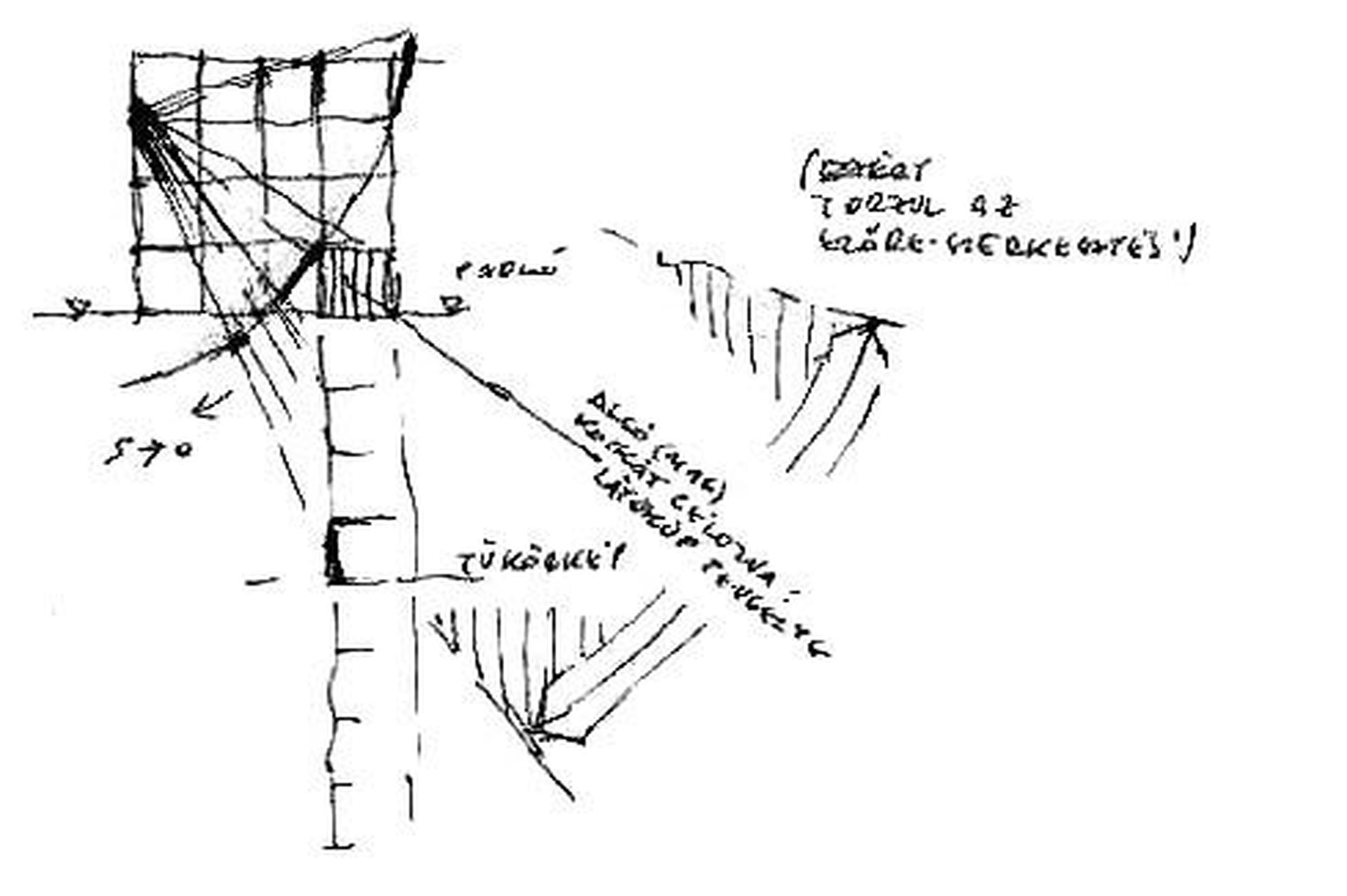
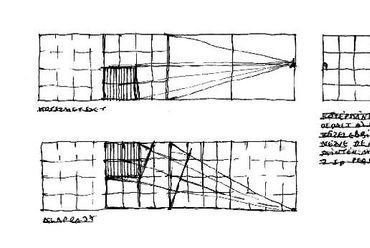
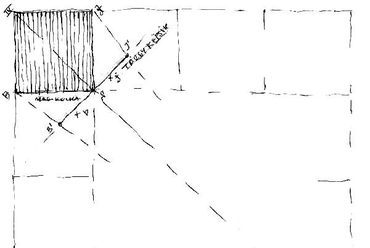
10. ábra: Vetületi segéd-ábrák a (C) esethez***. Felül a felezősík oldalnézete látszik, alatta az adat-másoláshoz megfelelően beállított, alaprajzi helyzet (Np = nézőpont, Vs = vezérsugár, TKs = tárgy-képsík, xb ill. xj= baloldali ill. jobboldali oldallap metszéke).

Érdemes az alaprajzot az előkészítő fázisban úgy forgatni, hogy arról akár közvetlenül is átmásolhassuk a vezérsugár (Vs) hosszát, mint felezősíkunk talpvonalát! A felülnézetről levehetjük az oldallapok arányát (a nézőpontunkból látható baloldali ill. jobboldali, vízszintes irányban mért kockaél-távolságok, ahogy azok megjelennek a tárgy-képsíkon). Ugyanitt tűnik fel a hátsó (IV.) él helye is. Ezt a kiegészítő adatot első kockánk felvázolásánál kitűnően hasznosíthatjuk.

Az ábra felső részében elhelyezett metszetről a kocka-torony alsó lapjának torzulását (TR = talp-rövidülés, FR = fedlap-rövidülés), ill. fedlapjának látszólagos helyzetét vihetjük át készülő szerkesztésünkre - papírcsíkkal [3]. Ezek az arányok elsősorban a szélső kocka befoglaló méreteit határolják be.

***Dr. Méhes B: "Első kocka - szélső kocka" (Vetületek hasznosítása a szerkezeti alapvonal-háló kezdő kockájához), 2004 [3],

Képsík, térsarok, iránypont

Gyakran elhangzó hallgatói kérdés, hogy "adott nézőpontból hány iránypontunk lesz?" Az iránypontok száma a szemlélő képsíkja és a térsarok lapjai közti viszonytól függ. Iránypont akkor keletkezik, amikor képsíkunk metszi a rácson át szemlélt sík párhuzamos vonalsorozatát [2].

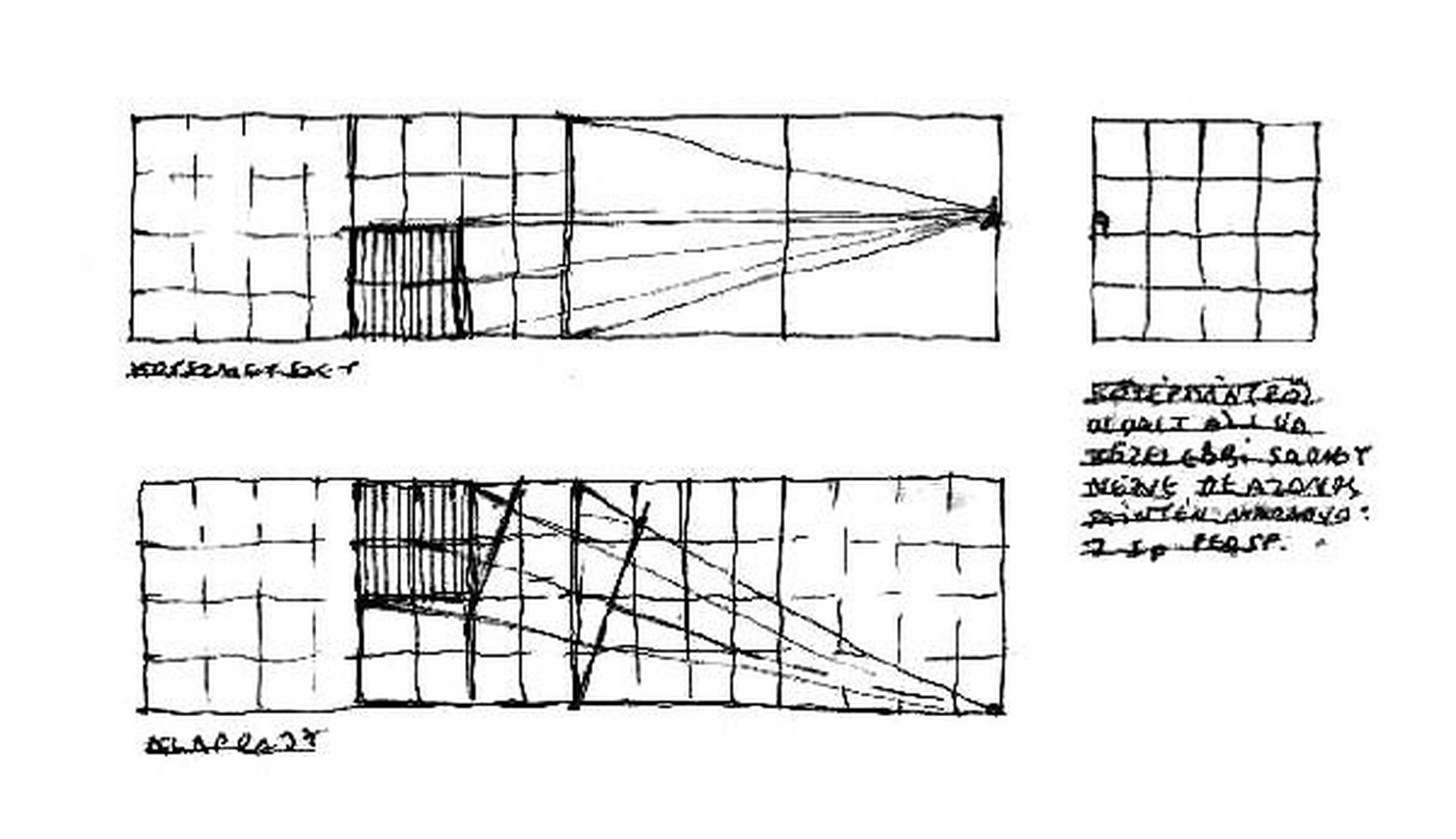
Amíg képsíkunk az egyik lappal párhuzamos, a másik kettőhöz képest merőleges (pl. a távoli hátfal felé nézünk), a nagykocka-belső szerkezeti felépítéséhez egy iránypont elegendő (A eset, de ide illik a B helyzet is, mint határeset).

Amikor merev nyakkal, lassan elfordulva, képsíkunk az egyik kockalapra még merőleges, de a másik kettővel már szöget zár be, két irányponttal dolgozunk (C eset).

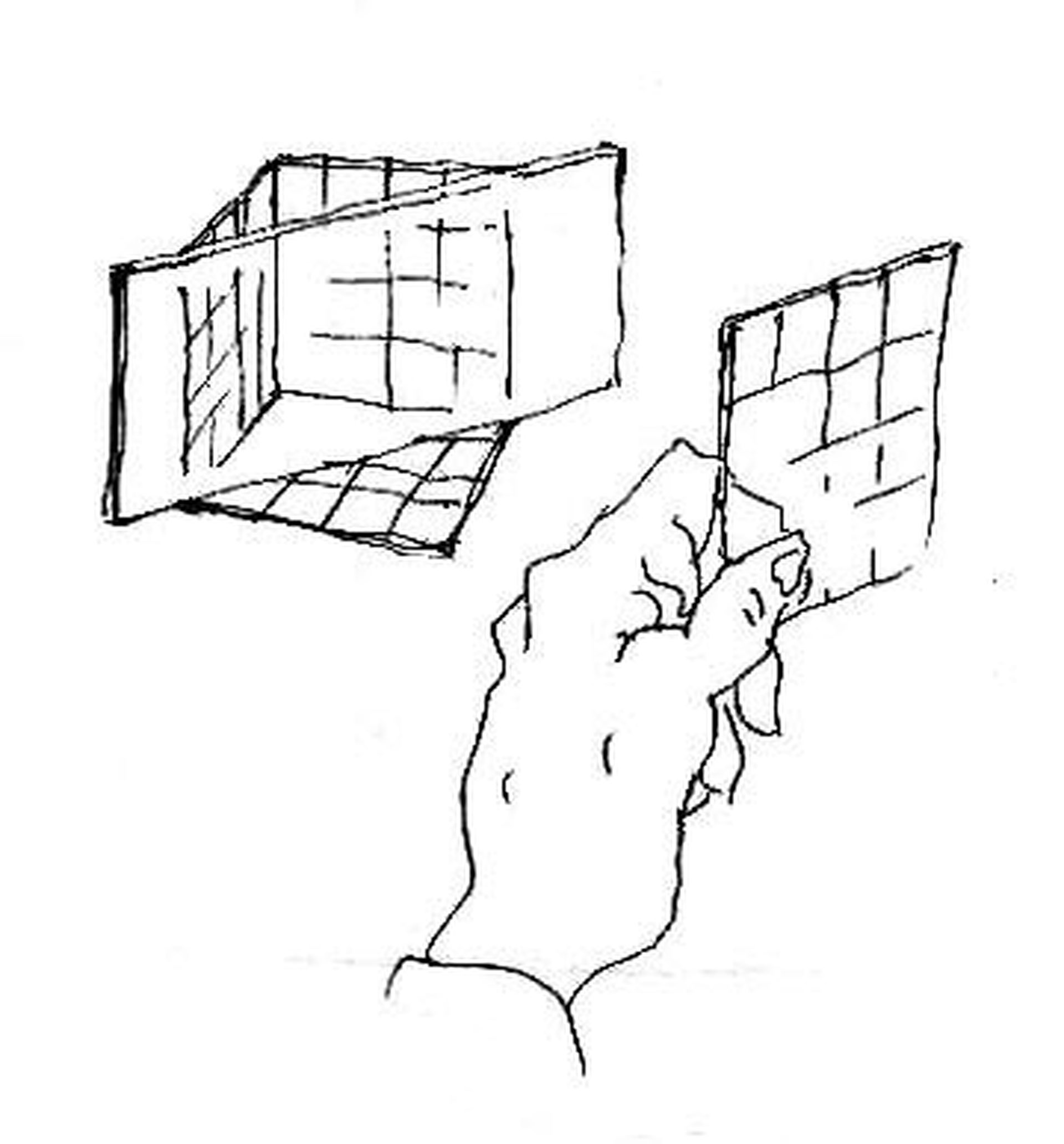
Amikor fejünket megdöntve, tekintetünket egy közeli sarokba irányítjuk, azt tapasztaljuk, hogy a függőlegesek is megbillennek. Ha képsíkunk mindegyik térbeli főiránnyal szöget zár be (egyikkel sem párhuzamos, de nem is merőleges), három iránypontunk lesz (D eset).

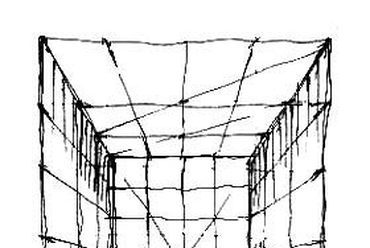
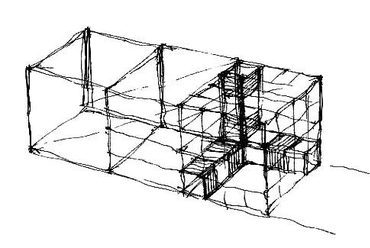
13. ábra: Egy másik emelet felé, vagy egy közeli térsarokba nézve, képsíkunk mindegyik térbeli főiránnyal szöget zár be (azaz egyiklappal sem párhuzamos, de nem is merőleges), - ez a három iránypontos perspektíva esete.

A hátfal irányába, távolra tekintve, amíg csak egy irányponttal volt dolgunk (A és B eset), az idézett füzetben [1] ismertetett módszer kielégítően működött. A (C) és (D) esetben viszont, amikor közelebbi sarkok felé tekintünk, látókörünkből kicsúsznak a nagykocka sarkai. A rajzon kívüli iránypontok bizonytalanná teszik a szélső ferdék dőlését. Perspektívánk további sorsa a megcélzott térsarok (Y-csomópont) tengelyeinek sikeres beállításához kötődik.

15. ábra: Modellezett (D) helyzet. A vetületekre terített négyzetháló után, minden nézeten bejelölve a célba veendő első kockát, készítsünk kis modellvázlatot, mintha madártávlatból szemlélnénk a szerkezeti rácsot! Kívülről elképzelt szituációban tisztán megjeleníthető a "térsarok-mérce". Javasolt módszerem szerint a közeli nagykocka-sarokba kiskocka-füzért illesztünk, melynek szívében ott rejtőzik a megcélzandó "mag-kocka". Az első kocka gondos megrajzolása után szomszédjait az "átlós módszerrel" hozzuk létre.

Dilemmánk az eredeti háló tovább-osztásával oldható fel - a hozzánk túl közel került nagykockát egy kiskocka-sorozatból álló, sarokba illesztett rács-töredékkel helyettesítjük. Ahogy egyszerűbb eseteknél beköltöztünk a felnagyított kocka belsejébe [1], ugyanígy vissza-zsugoríthatjuk az ábrázolandó teret modell-szerű, kívülről rajzolható tárggyá, amikor több irányponttal dolgozunk.

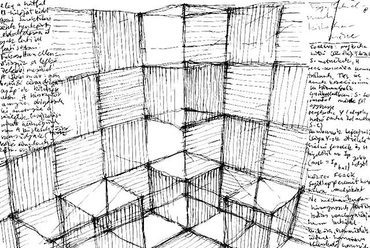
17. ábra: Térsarok-építés nagykocka sarkába illesztett kiskocka-sorozattal. Átlós módszer a szomszéd egységek rácspontjait hozza. Azonos síkbeli sarkok szerkesztéséhez használjuk fel a vonatkozó átlók iránypontját is! Negyed-pontokhoz sorozatos "átlós felezésekkel" jutunk el.

Kiskocka-füzéreket illesztünk a közeli nagykocka hátsó sarkából kiinduló élek mentén. A választott térbeli csomópont legbelső kockája a "mag-kocka". Innen kezdve szokásos tárgyrajz esetével van dolgunk. Az Y-csomópont magjában lévő "mag-kockát" kell jól eltalálni, a többit tükrözéssel szabályosan szerkeszthetjük!

19. ábra: A "felezősíkról" levehető a mag-kocka alaplapjának rövidülése (elülső "álló" ill. hátulsó "fekvő" él metszéke). Ugyanerről a speciális metszetről átvehetjük a nézőpontunkkal azonos magasságban lévő egység fedlapjának rövidülését is (nagy Y / S4). Folyamatosan kövessük betű- vagy számjelekkel az élek ill. sarkok helyzetét! Nézőpontunkból célozzuk meg a mag-kocka súlypontját! A tárgy-képsíkra merőleges vezérsugár a szemlélő és a leképezendő tárgy közötti legrövidebb távolságot jelenti. A tárgy-képsíkon leolvashatjuk a közeli, függőleges él rövidülését.

Segéd-vetületeink részletezése

A szabadkézzel megrajzolandó "első kocka" perspektívikus helyessége nem csak tapasztalatunkon (népszerűen fogalmazva: hasra-ütésen) múlik! Hasznos adatokat nyerhetünk a megfelelően előkészített segéd-vetületeinkről [3].

Az előkészítés során pontosan tisztázzuk, mit és honnan célzunk meg vezérsugarunkkal? A szerkezeti váz végső eredménye elsősorban a mag-kocka hihetőségén múlik. A vezérsugár(Vs) és a tárgy-képsík (TKs) mindkét vetületre berajzolandó. A felezősíkra (FS) állítandó metszet úgy készül, hogy az alaprajzról átmásoljuk a vezérsugár hosszát. Ez lesz a felezősík padlószintje. A felezősík az alaprajzra merőleges, talpvonala a vezérsugár első képe. Ezen a vetületen mag-kockánk téglalap-alakúnak látszik. Mostani átlós helyzetében befoglaló formája éppen 1 x gyök 2. A rálátás arányát a felezősíkról olvashatjuk le.

Ha a nézőpontunkhoz túl közel esik a mag-kocka, bekövetkezik a III. iránypont esete. A korábban függőleges (S1-4) közeli élek rövidülései rendre leolvashatók a felezősíkon. Adatgyűjtés közben mindig az illető kocka súlypontját célozzuk meg a vezérsugárral! Az emeletek (negyed-kockák) magassági változásai:

• A negyedik szint egységnyi maradt (S).
• A harmadik szint rövidülése elhanyagolható.
• A második szintnél kb. 9/1o a méretváltozás.
• Az alsó szinten nagyon látványos a magasság csökkenése (kb. 4/5).

A szélső kocka befoglaló formájának hozzávetőleges méretei az alaprajzról és a felezősíkról rendre leolvashatóak (xb+xj / S, illetve "nagy Y" / S).

Összegezzük végül a térsarok-mérce vázolási sorrendjét:

• X, y, z tengelyek (a térbeli Y-csomópont ágai)
• Magassági skála beosztása (rövidülő S-szakaszokat papírcsíkkal átvéve a felezősíkról)
• A szemsík (H) bejelölése a magassági skálán (itt: felső negyed alsó harmada tájára esik)
• Alsó kocka befoglaló formája: oldalmetszék-arány az alaprajzról, továbbá a talp-lap rövidülése ("nagy Y") a felezősíkról átvéve. Az alaplap hátsó (IV.) éle és a közeli S metszéke szintén leolvasható.

Ne felejtsük el, hogy a segéd-vetületekről nem abszolút értékeket, hanem arányokat viszünk át perspektív vázlatunkra! (Ha elég nagy vetületeket gyártanánk, bizonyos értékeket közvetlenül is átmásolhatnánk papírcsíkkal.) Fontos, hogy mindig ugyanarról a mérőképsíkról vegyük le a változó S adatait!

Egyik legfontosabb metszék a szélső kocka magassági rövidülése - a legtávolabbi négyzetlap nagy ipszilonja az S-hez képest (itt: kb. ¾). Bár a fedlap karcsúsodását közvetlenül is leolvashatnánk ezen a speciális oldalnézeten, a gyakorlatban inkább azt az elvet kövessük, hogy a szélső ferdék (és a horizont) által meghatározott iránypont segítségével a köztes ferdék maguktól adódnak. A mag-kocka fedlapjának kontúrvonalai ebbe a kategóriába esnek.

A felső kiskocka (negyedik szint) nagy Y-ját is leolvashatjuk (itt: felső ¼). Ezen a szinten az alaprajzi össz-szélesség (SZ) éppen kb. gyök kettő volt. A sarok-mérceként szereplő torony teteje a velünk egy magasságban lévő kockánál kb. 1: 6/5, alja pedig kb. 1: 4/3, vagyis a karcsúsodás nyilvánvaló. Lefelé haladva, szemsíkunktól egyre inkább távolodva, az S csökken; a mélybe tekintve, rohamosan tart a 0 felé!)

Mivel az oldal-metszékek aránya nem változott, (SZ= xb + xj és a vizsgált emelethez tartozó közeli függőleges él viszonya állandó), ezért a két szélső, azaz a legfelső és legalsó kockán azok befoglaló formáját felvázolva, egyértelműen kialakul a függőlegesek megbillenését jelző összetartás.